从今天开始我准备写一系列有关于排序算法的文章，当然不止排序算法，以后还会写其他的算法。自己算法方面薄弱，大一上数据结构课的时候也没有好好听课，更别说学了。所以从这篇文章开始，我会巩固一下算法，并写一系列的算法文章，写文章的好处在于把所学知识梳理成章，并且希望可以帮助其他同学。

由于自己水平有限，开学后各种事情也比较多，文章可能会有纰漏，望各位批评指正。

同时，在各类的排序算法中，我们应把注意力放在算法本身，为简单起见，示例代码均使用 int 数据类型，且均为升序排列。

算法简述

算法，何为算法？

定义

算法(Algorithm)是为了解决某类问题而规定的一个有限长的操作序列。

特征

• 输入：一个算法必须有零个或以上的输入量。
• 输出：一个算法应有一个或以上的输出量，输出量是算法计算的结果。
• 有限性：一个算法必须总是在执行有限步后结束，且每一步都必须在有限时间内完成。
• 确定性： 算法的描述必须无歧义，以保证算法的实际执行结果是精确地匹配要求或期望，通常要求实际运行结果是确定的。
• 可行性：即算法能够实现，算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。

冒泡排序

冒泡排序(Bubble sort)是一种最简单的交换排序算法。大概是所有程序员都会用的算法吧。

算法思路

假如有 n 个元素要进行排序。

n = 1:

无需排序。

n > 1:

• 第一轮排序

  比较相邻两个元素，如果第一个比第二个大，则交换两个元素的值。
  进行下两个元素的比较，即比较第二个和第三个元素，如前者大于后者，则交换。
  再进行下两个元素的比较。直到第 n-1 个元素和第 n 元素进行比较，如前者大于后者，则交换。
  可以肯定，最后一个元素 n，肯定是 n 个元素中最大的元素。

• 第二轮排序

  重复执行第一轮执行的动作，直到第 n-2 个元素和第 n-1 个元素进行比较。如前者大于后者，则交换。
  由于第一轮排序已经将最大元素放置到第 n 个位置，所以本次排序无考虑第 n 个元素。即第 n 个元素不参加本次排序。
  .....
  示例图片:

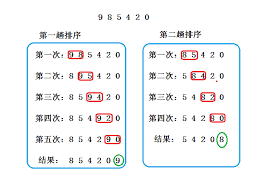
• 重复执行

  直到只剩一个元素，那么这个元素一定是最小元素，排序结束。显然，进行了 n-1 次排序。

上述过程，每次排序(即每轮排序)都会有一个元素从某个位置慢慢“浮动”到最终所属的位置,就像气泡总会浮动到水的最顶端。在冒泡排序中，每一轮排序都会有一个元素(气泡)替换到本次排序的最后一个位置(水的最顶端)，注意，是本次排序的最后一个位置(第一轮，则为 n；第二轮，则为 n-1；第三轮，则为 n-2 ~~~ )。

因为，排序的过程像是冒泡一样，则称为“冒泡排序”。如下为冒泡排序示意图(来自维基百科)

代码实现

设要给数组 arr[] 排序，它有 n 个元素。

public static void bubbleSort(int[] arr) {
    int temp = 0;
    for (int i = arr.length - 1; i > 0; --i) { // 每次需要排序的长度
        for (int j = 0; j < i; ++j) { // 从第一个元素到第i个元素
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

算法优化

假如有一组数据为：1,2,3,4,5,6,7,8,9,0。 如果用上面的方法实现排序会有什么情况，当然，实现排序肯定没有问题。但是，这组数据的前面一大部分已经是有序的了，如果还是用上面的代码会使效率降低很多(数据比较大的情况下)。所以，将代码进行优化。

public static void bubbleSort(int[] arr) {
    int temp = 0;
    boolean swap;
    for (int i = arr.length - 1; i > 0; --i) { // 每次需要排序的长度
        swap=false;
        for (int j = 0; j < i; ++j) { // 从第一个元素到第i个元素
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swap=true;
            }
        }
        if (swap==false){
            break;
        }
    }
}

在实际使用过程中，由于在大量数据的情况下几乎不使用冒泡排序，而使用小数据的时候增加的布尔变量反而会造成额外的开销。通常，冒泡排序就使用前一种就行了。

算法复杂度

• 时间复杂度

  当最好的情况，也就是要排序的表本身就是有序的，那么我们比较次数，根据最后改进的代码，可以推断出就是n-1次的比较，没有数据交换，时间复杂度为O(n)。当最坏的情况，即待排序表是逆序的情况，此时需要比较 n(n-1)/2 次，并作等数量级的记录移动。因此，总的时间复杂度为O(n^2)。

• 空间复杂度

  由以上算法步骤分析，可轻易得知冒泡排序的空间复杂度为 O(n), 需要辅助空间 O(1)

算法稳定性

容易看出，在相邻元素相等时，我们并不需要交换它们的位置，所以，冒泡排序是稳定排序。

算法适用场景

在算法优化中提到过，实际使用过程中，在大量数据的情况下几乎不适用冒泡排序。冒泡排序思路简单，代码简单，特别适合小数据的排序。但是，由于算法复杂度较高，在数据量大的时候不适合使用。